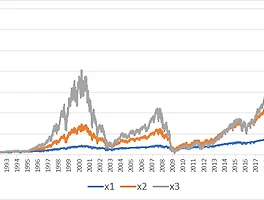
Kelly Criterion calculates the optimal betting fraction given the expected outcome and probability for both negative and positive scenarios. Optimal means the highest expected geometric return. The proof follows below.

This is intuitive as an exponential function with an exponent less than 1 is concave. Thus the graph's marginal growth is decreasing. Also, note that geometric mean is approximately arithmetic mean minus one-half of the variance which can be derived by 2nd approximation of the Maclaurin series.
Note that when Sharpe ratio is calculated with arithmetic mean, any betting size will lead to the same Sharpe ratio. This is one reason why it makes more sense to target a specific volatility than a specific return in calculating the betting size (or the leverage ratio).
'Basics' 카테고리의 다른 글
| 증권사 vs 운용사 vs 헤지펀드 (0) | 2021.10.24 |
|---|---|
| Sector Breakdown of Major Equity Indices (2021 Jul) (0) | 2021.09.13 |
| 투자자가 변동성을 높이고 레버리지를 일으켜야하는 이유 (1) | 2021.03.17 |
| 운 vs 실력,노력: 간단한 통계적 실험 (0) | 2020.09.03 |
| 추천 투자 유투버들 (0) | 2020.09.02 |