Fixed Income as the name implies, usually provides a fixed amount of cash flow to the investor. There are some mathematical structures to be noted when looking into fixed income products.
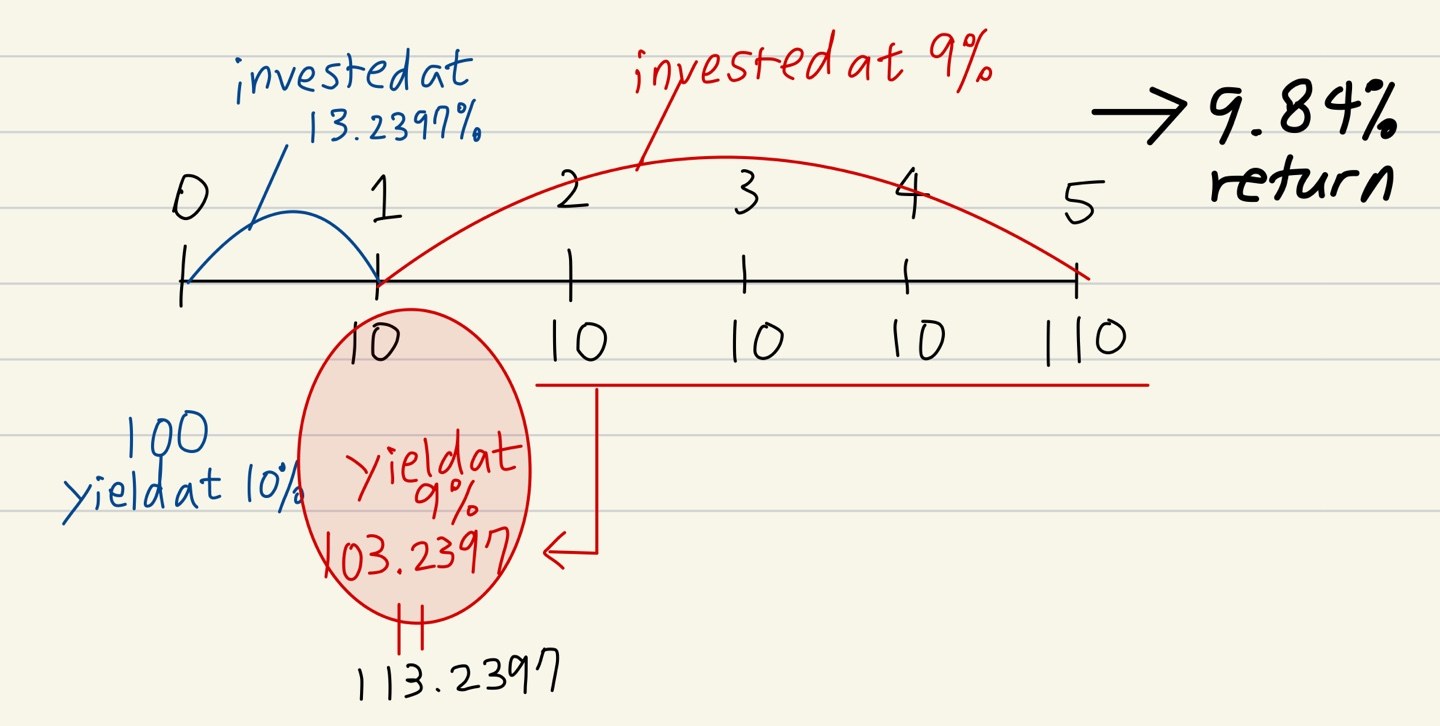
The price of a Fixed Income is priced by discounting the future cash flows by the current market yield which is yield to maturity. Let's assume, there is a bond that gives 5% coupon. This does not mean, you are guaranteed to get annualized 5% return at the maturity day because it would have to be reinvested at 5%. This is called "reinvestment risk." The present value of the bond will change by the discounting interest rate. This is called "price risk." They always offset each other. So if market yield changes from 5% to 3% while holding the bond, the total realized return for the investment will be the same (in between 5% and 3%) whether you keep the bond to maturity (while reinvesting the coupons) or sell the bond and reinvest in whole.
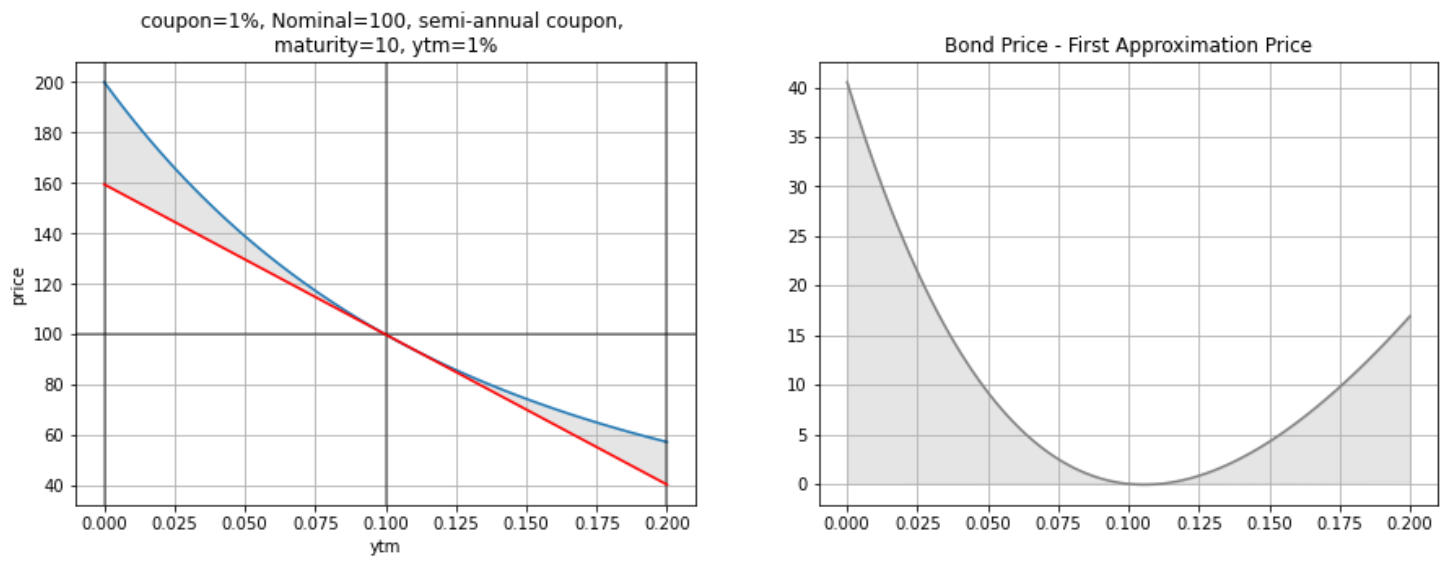
1) Bond price is inversely related to the ytm
2) Bond price will rise more as yields fall than linearly expected. In the same manner, the bond price will fall less as yields rise than linearly expected. This is because of the convexity effect.
3) While the second-order effect is symmetric, Due to higher-order (>2) effects, the "bond price - first approximation price" is not symmetric. This means that first approximation is more accurate when yield goes up than when yield goes down. (this is a rather complicated explanation - simplistically just think about compounded discounting) This also means that for example -50bp change = +50bp +alpha change in terms of the price changes in the bond. -1bp is a bigger impact than +1bp change.

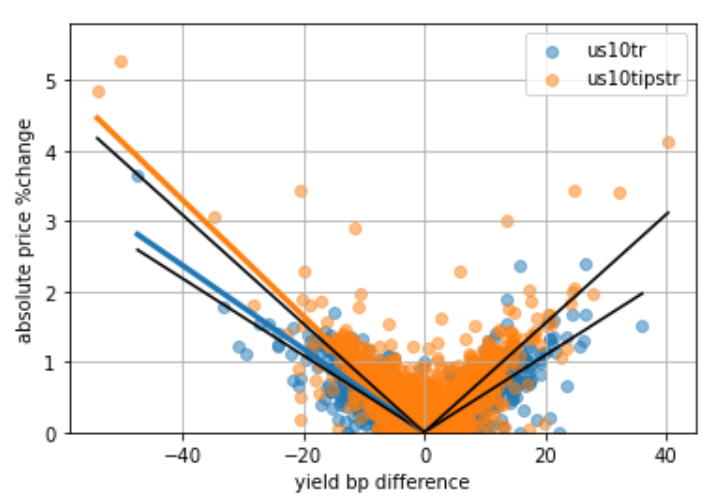
As ytm and coupon decrease, duration increases, thus, price changes become more sensitive to same amount of basis change in ytm.
If the maturity is the same, convexity is lower for higher coupon bonds, meaning convexity is highest for zero-coupon bonds.
Even if the Modified Duration at a given ytm is the same, Convexity can differ.
Compare two bonds
- Bond A: coupon 14.6%, Face Value 100, semi-annual, maturity 7, ytm 10%
- Bond B: coupon 1%, Face Value 100, semi-annual, maturity 5, ytm 10%
Both Bond A and Bond B have the same modified duration of 4.414. However, convexities calculated by the 2nd moment divided by (current price*2) are respectively 14.310 and 11.997. This doesn't mean there is an arbitrage opportunity as this is not only artificially made, ytm will change differently for each of the bonds.
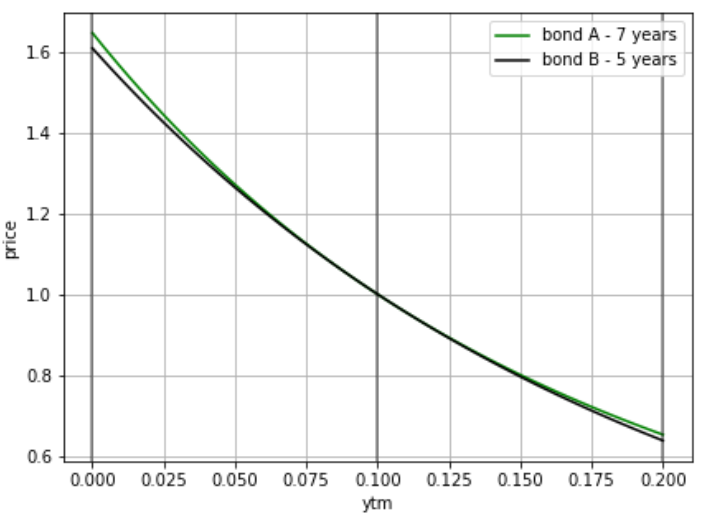
< Analyzing historical series to calculate convexity >
It should be noted in advance that convexity is just a function of duration and the current yield level. So analyzing this only using historical yield series and total return series has a lot of caveats. One method to calculate the convexity is to first do a linear regression and take off the slope effect and then fit with a squared term again. However, if the yield movement was bigger when the yield level was high and yield movement was smaller when the yield level was low, the calculated convexity would give a minus value.
'Financial Math' 카테고리의 다른 글
| Quant Interview examples (0) | 2021.07.23 |
|---|---|
| Efficient Frontier (0) | 2021.04.18 |
| 금융 로그리턴, 심플리턴 (0) | 2021.04.07 |