#1
[ Question ]
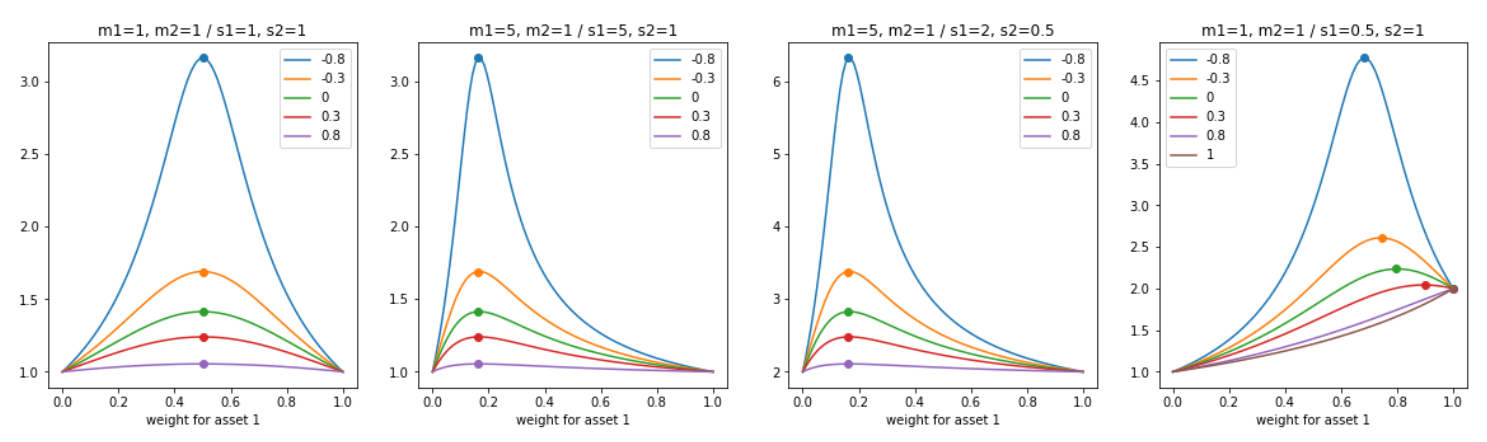
There are two assets with the same expected return and the same expected variance. What is the optimal portfolio weight?
[ Answer ]
If the objective is to maximize the ratio of expected return and the expected standard deviation, always mix them half and half unless rho equals 1. If rho equals 1, weight does not matter as the objective ratio will always be independent of the weight.
[ Extension ]
- If sharpe ratio is the same but asset 1 has expected return and standard deviation that are n times that for asset 2? In this case, the optimal weight for asset 1 would be 1/(n+1). If rho equals 1, weight does not matter as the objective ratio will always be independent of the weight.
#2
[ Question ]
If the correlation matrix has the same values for the correlation part of the matrix, what is the possible range for the correlation value?
[ Answer ]
step 1) the correlation matrix (omega) can be decomposed into (1-rho)*I + rho*M where I is the identity matrix and M is a ones' matrix.
step 2) eigenvalues of M are either 0 or the size of M = n if nxn matrix (M * v = lambda * v)
step 3) omega * v = (1-rho) * v + rho * lambda * v = (1 - rho - rho * lambda) * v -> eigenvector of M is also the eigenvector of omega.
step 4) so the eigenvalues of omega are either (1-rho) when lambda is 0 or (1 + (n-1)rho) when lambda is n
step 5) positive definite matrix must have non-negative eigenvalues
step 6) the condition yields, -1/(n-1) <= rho <= 1
'Financial Math' 카테고리의 다른 글
| Fixed Income Basics (0) | 2021.07.24 |
|---|---|
| Efficient Frontier (0) | 2021.04.18 |
| 금융 로그리턴, 심플리턴 (0) | 2021.04.07 |